Newton's rings : EXP200080
Référence : EXP 200 080
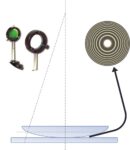
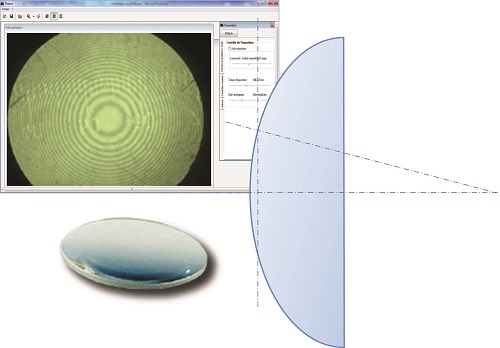
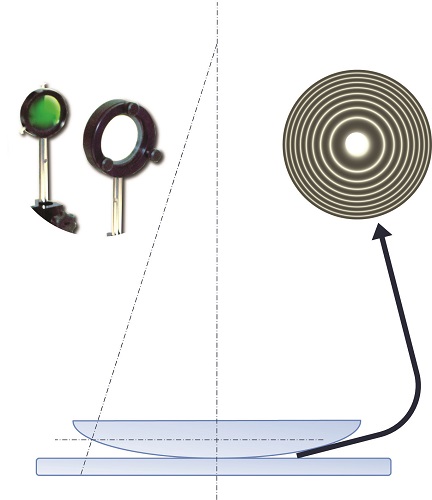
A very slightly convex lens is placed in contact with the flat surface of a glass slide. It then forms an air wedge with a curvilinear boundary surface. If the device is illuminated with an incident light with parallel rays, concentric interference rings are formed around the contact point of the two surfaces. The distance between the interference rings is not constant since the air wedge boundary surface is curvilinear. In this case we shall use a sighting device for our measurements. We can combine this device with a webcam to retrieve data on a computer.
RADIUS OF CURVATURE
The Newton’s rings device yields rings in view of its rotational symmetry. Another difference is highlighted by the type of
reflections involved. Reflection is of the glass-air type on the spherical diopter of the lens, and of the air-glass type on the
mirror.
Newton’s rings are in this case observed in transmission as the flat plate is transparent. The central ring is thus bright.
AIR WEDGE
We illuminate at normal incidence, with a monochromatic parallel beam of light, a large-radius convex flat lens placed on
a glass slide. Part of a ray is reflected on the glass-air interface without phase change, while the other part passes through this interface, and a fraction of this ray is reflected on the bottom slide. As this ray is reflected by a more refractive medium, this reflection produces a phase shift of π. These two reflected rays, of adjacent amplitudes, interfere by yielding localised fringes (as for thin plate) in the vicinity of the lens spherical surface. Let R be the radius of curvature on the underside of the lens. In other words r = OI is the distance between the ray and the optical axis of the system.
As r is far smaller than R, we obtain: e ≈ r2 / 2R. The optical path difference is formulated as δ = 2e + λ / 2 = r² / R + λ / 2. As the system accepts an axis of revolution, fringes are rings centred on this axis. Dark rings are obtained when δ = (2k +1) λ / 2 or for 2e = r2 / R = kλ. If the lens is in optical contact with the underside, the first ring will be dark. The following rings (the optical path difference increases by one wavelength between two rings) have radii proportional to the square root of an integer.
SUBJECTS APPROACHED
»»Air wedge
»»Radius of curvature
NECESSARY EQUIPMENT
COMPOSITION
EXP200081 Newton's rigns (BASIC)
| Référence | Désignation | quantité | | POF010112 | 1-m Prismatic optical bench | 1 | | POF010124 | Optical rider | 3 | | POF010126 | Optical rider with horizontal motion | 1 | | POD066061 | Newton's rings device | 1 | | DPO020020 | Power supply for ECO27 Spectral lamps | 1 | | POF010062 | ECO27 Mercury lamp (bulb only) | 1 | | POD010572 | Green interference filter- 546 nm | 1 | | POD069440 | Viewfinder | 1 | | POD061250 | Dual Condenser | 1 |
COMPOSITION
EXP200080 Newton's rings (COMPLETE)
| Référence | Désignation | quantité | | POF010112 | 1-m Prismatic optical bench | 1 | | POF010124 | Optical rider | 3 | | POF010126 | Optical rider with horizontal motion | 1 | | POD066061 | Newton's rings device | 1 | | POD010030 | Pedagogical webcam | 1 | | DPO020020 | Power supply for ECO27 Spectral lamps | 1 | | POF010062 | ACO27 Mercury lamp (bulb only) | 1 | | POD010572 | Green interference filter- 546 nm | 1 | | POD069440 | Viewfinder | 1 | | POD061250 | Dual condenser | 1 |
Computer is required for the webcam
|
|
Mon compte
